お問い合わせ
075-322-7088 
CASE
開発事例
物体の回転角度評価
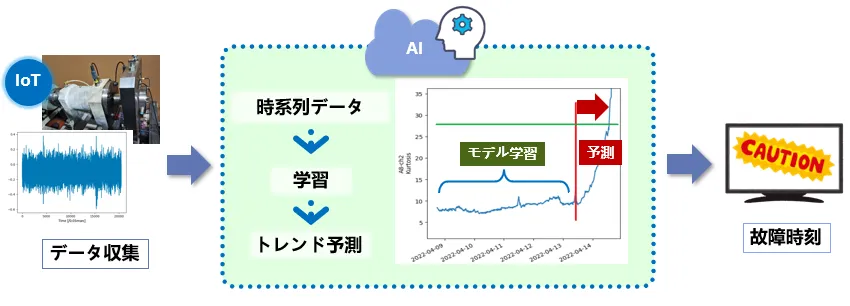
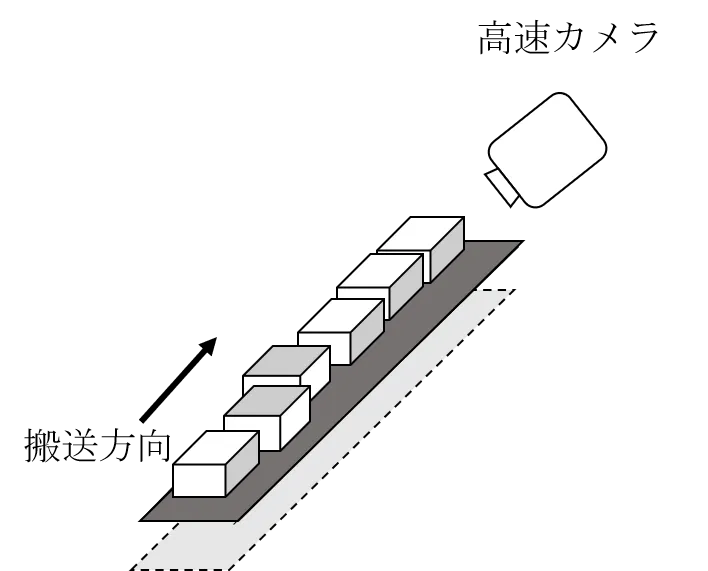
搬送装置を高速で流れる物体の画像を撮影し、向きや姿勢を瞬時に判断、間違った状態にある物体は制御装置を介して選別、修正するための手法です。整列された物体は効率よく処理されますが、そうではない物体を選別して排除したり、姿勢を修正したりする必要があります。
選別装置には、エアージェット、トリップ、プッシャーなど様々な方式がありますが、そのときの物体の姿勢を評価して修正（フィードバック）をかけることで、状況に応じた最適化が可能です。物体の姿勢は主に回転角度に反映されますが、整列されていない物体の選別、あるいは選別された物体の姿勢を修正するために、回転角度情報を利用します。歩留まりにも直接影響するため、いかにして正確に回転角度を推定するかが重要となります。
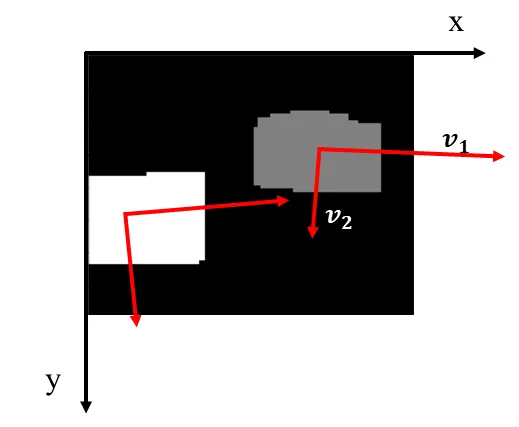
回転角度評価を行うには、まず物体の動きを追跡します。フレーム毎に位置を認識し、前後のフレーム間で最近傍での対応付けなどを行う前処理（2値化やMorphingなど）を行います。
撮影した物体の画像データから得られた2次元の共分散行列を考えます。X=[x,y]を点群のx,y座標を並べた行列とすると
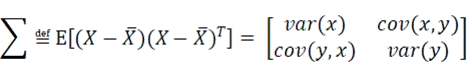
∑はx,y座標の相関関係、つまり点群の伸び具合を意味します。
一方、特異値分解を適用することで、点群の主軸とそれぞれの長さ（固有ベクトルと固有値）が算出できます。与えられた行列Mを固有値と固有ベクトルに分解します。
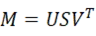
ここで𝑈と𝑉は固有ベクトルを含む直行行列で、Sは固有ベクトルに対応した固有値です。
最後に主軸の位置合わせを行い、t 番目フレームでの固有ベクトルと回転行列Rから、t+1番目フレームの回転角度𝜃を算出します。
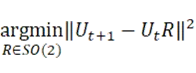
を目的関数、Ut はt番目フレームでの固有ベクトルであり、Rは回転行列です。
Rが回転行列（2次元の特殊直交群）のとき、特異値分解（SVD）による最適なRを求める手法が考案されています。
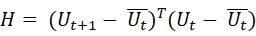
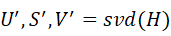
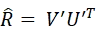
から回転角度𝜃を算出することができます 。
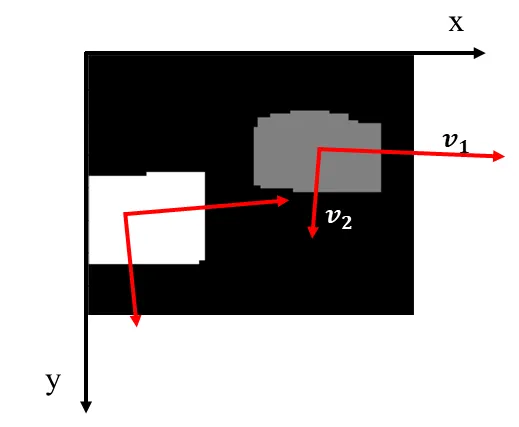
こうして求められた回転角度の情報を活用することで、搬送装置の制御を効率よく行うことができ、実際に装置制御の基礎技術として用いられています。
関連する記事一覧
2025.02.12
AI技術業務に特化した物体検出ソリューション：航空写真のマスキング自動化
2025.02.12
AI技術